What to do…

I have a bit of a dilemma.  Three years ago I was brought to a GATE magnet school to teach a bunch of advanced kids. 

The thought was, “Rather than ship the really smart kids to high school to take the geometry class, we’ll just bring the high school teacher to them.” 

I didn’t mind this idea.  In fact, it quickly began to grow on me.  I was teaching precalc, algebra 2 and algebra 1 at the high school and figured the change might do me some good.  The tough part was that I had no idea what to expect.  I was going from 55 minute periods to 94 minute daily blocks. 

What the heck am I going to do with a group of middle schoolers for 94 minutes? 

So after many discussions with my principal, we decided that since the 94 minute block was intended to allow for grade level instruction as well as time for intervention,  I’d just use my extra time for enrichment.  But what do you do to enrich them?  Do you accelerate the students so that they can be ready for algebra 2 as freshmen?  Do you spend the extra time doing all the cool stuff that no one else has time to do because they are worried about pacing guides and benchmarks?  We’ve decided to go ahead and accelerate them.  I’m still a bit unsettled about it, though.    Is it really that important for an 8th grader to complete geometry so she can take algebra 2 in 9th grade?  The kid is on pace to take calculus as a junior.  Is that better?  At this point, I don’t know.  In the era of “the TEST”, it seems that as long as I have the data to back up what I am doing, it doesn’t matter what we choose.  My kids have the test scores, but I am not convinced that what I am doing is the right thing. 

I am definitely in unchartered waters.  As a high school teacher, I was simply one of many.  My last year there, we had a pacing guide and all common assessments.  It was pretty lock step and I was miserable–loved the staff and the students–but hated the system.  Now I have a bunch of autonomy because I can keep the powers that be off my back with some good scores, but I am not sure what direction to go.

Last year, the decision was a bit easier because I got to hand pick the students who would move into the geometry class. I taught both advanced 7th grade classes so I knew they were ready.   This year–not so much.  I have two classes made up of kids from two different teachers.  Some are ready to be accelerated and others look like they are going to need to spend some serious time with the algebra.  My question for you all is this:  how do you plan for these classes?  Half of my students have already been through algebra, a quarter of them have been exposed to it and the rest look like they may not know what a variable is.  I’ve never been here before, so I don’t know what to expect.  If you’ve ever considered commenting on a post here, now’s the time.  Hit me up.

Chandler Saves the Day

You ever have a lesson that you thought was going to go pretty well only to have it fall flat?  Yeah, that happened today. 

My 7th graders have been going over quadratics for the past couple of weeks.  I have been out quite a bit on school business, so the progress has been slow, but very rewarding.  Last week, students discovered that if you change the value of “a”, it has an effect on how fast the parabola grows.  I then had them graph a bunch of parabolas whose line of symmetry was the y-axis only to have a student ask,

“Can we move the parabola left or right?”

“Well since you asked…”  So I did what any responsible teacher would…I had them graph a bunch of parabolas whose vertex sat on the x-axis which led to the next question,

“Can we move them up/down and left/right?”

So Friday, we are graphing parabolas in the form y =a(x-h)^2 +k and they are getting it.  This is stuff I couldn’t do until Algebra II with my high school students and these 7th graders are just crushing everything I throw at them. I would even give them a vertex and  a second point and they were giving me an equation because they figured the stretch factor using the second point.  Things are looking good and I am thinking:

Man this is just toooo easy…

Yeah, I know, pride comes before the fall.  Which is what started to happen today.  I have had a planning block.  Now that we have graphed a bunch of parabolas in vertex form, where do I go from there?  Do I start dealing with standard form? Do I show them how to expand (x-h)^2 in order to arrive at standard form?  I am still not sure what the ideal path would be.  But being the “try anything once” kind of guy I am, I figured that since I have already had them:

• Graph quadratics organically (area vs. radius; area vs. side length)
• Graph quadratics with a not equal to 1.
• Graph quadratics with vertex on y axis.
• Graph quadratics with vertex on x axis.
• Graph quadratics in the form y = a(x-h)^2 +k

…then I would focus in on what was necessary to graph a parabola:  vertex and stretch factor.  If they could identify the vertex and a stretch factor, they can graph anything, right?  So today I wanted them to graph a bunch of parabolas in standard form, look for the line of symmetry and recognize the relationship between a,b and the line of symmetry.  I didn’t expect them to necessarily “discover” that the line of symmetry is x = -b/(2a), but I figured that if we graphed enough of them, we might start to notice some patterns.  Once we have the line of symmetry down, then we could start looking at x intercepts which would lead us to factoring and completing the square as well as quadratic formula.  (If my sequencing on this is bad, please save me from myself. )

This is where it started to go bad.  GeoGebra is a great program, but it doesn’t save a weak lesson.  Kids were all over the place with their parabolas and we were getting lines of symmetry like x=.7923496, which wasn’t going to help at all.  I was about to put us all out of our misery and jump ship when Chandler says, “Mr. Cox come here, I think I found something.” 

She had about 10 parabolas that all had the same line of symmetry.  She was making adjustments to the a and b values and recognized that the c value had no effect on the symmetry. So rather than aborting the mission, we just changed course. 

“How about choosing a line of symmetry and keeping the vertex on that line?”

They got right to it.  Tomorrow they are going to come to class with five different a,b,c values and the corresponding line of symmetry.  We will see where it goes. 

Note to the reader:  Quadratics are not a 7th grade standard and these kids will go through it on a deeper level as 8th graders.  So, I am not worried about “finishing” this with them.  I have the flexibility to let concepts marinade for a while.  Usually, I would have just followed the pacing of the book, but I have become very dissatisfied with that.  I am pretty sure that I want to continue from linear relations right into quadratic relations and that graphing is a good gateway to all the other skills that go along with quadratics.  I am just not sure how one skill will best lead into another.  Any suggestions?

Note to self: Quit gettin’ ahead of yourself and be sure to see the lesson through the eyes of a student rather than your own. 

Oh yeah, and thank Chandler.

No, Seriously… I Need Your Help

Alright, my head is about to explode.  For the next two days I’ll be sitting here in a room all alone trying to figure out how the heck we are supposed to bridge this gap. I have all the tools ready to go(computers, legal pads, pens, state framework,etc.). And all of a sudden it hits me.  The rules of math have come about because they were necessary.  For example, Natural numbers work until you try to subtract.  Then you have to have integers. Integers are fine until you divide, which leads to Rational numbers.  The Rational numbers  break down when you try to find the side length of a square with an area of 15.  Take the kids on this tour and we get to say: “Okay class, we have just discovered the Real Number system.”

We have exponents and scientific notation because it get really tedious to multiply (5,000,000,000)(8,000,000) by hand.  We introduce the symbols and variables because we don’t want to have to work out every single case for every single situation. We generalize because mathematicians are inherently lazy.  We truly find the shortest distance between two points. Kids are inherently lazy; they know the shortest distance between homework and their XBox.  Hey, we have someting in common.  How do we expolit that commonality in order to have kids “discover” algebra for themselves? How do we scaffold our entire curriculum, so that kids move from the Natural Numbers to Projectile Motion in such a way that they actually see how there is a need for it?

I realize that I am probably not saying anything you all haven’t already discovered for yourselves.  But, before I go and reinvent this wheel, I would like to know what you have all been doing to get this Algebra bus rollin’.

Dear Dan,

You are really starting to make me angry.  I was content to just do my job, help as many kids as I could, do some extra stuff to help them make it connect to their reality.  And then at 4:00pm shut it down, go home, kiss my wife, play with the kids, have a nice dinner, watch a little TV and go to bed.  But no!  You just had to start in with all this “using pictures to help kids learn math” stuff.  You couldn’t leave well enough alone.  When I couldn’t get Graphing Stories to work, you couldn’t just say “sorry dude, I am not sure why those chapters won’t play.  Better luck next time”… no you had to send me a copy and not even take the reimbursement I offered.  Who do you think you are?

Man I can’t even go to Target with my family without trying to take a picture of something.  You know how disruptive that is?  You know how hard it is to hold the baby, push the cart and snap a pic at the same time?  I am looking into having an extra arm grafted onto my torso.  You think my insurance will cover that?  Nooooo! And it is all because of YOU! 

The worst part is that I have these video cameras lying around my classroom and a blue screen in the library so I had to skip lunch the other day and take some footage that has resulted in some stills like these:

 

 

 I mean, look at that.  How can they not see that the ball is accelerating as it falls?  I don’t want that.  I want them to depend on me to tell them that gravity is an acceleration.

I'm not mad at you for this one, I actually think it's pretty cool.

What’s even worse, is I have all this raw video footage and I have no friggin’ idea what to do with it. What am I supposed to do, have students graph the height of the ball vs. time and realize that there are some relationships that aren’t linear?

My students are even getting into the taping.  They look so cute  and happy throwing the ball back and forth, but little do they know that one day this concept of math actually helping them  to interpret the world around them can consume them.  What’s next?  Are we going to start treating mathematics like a humanity and sit around discussing it as if it were a piece of literature or work or art?  Don’t you know that math is only supposed to be important  8:20-2:55 in Room 405 from September to June?  Don’t you know that math is supposed to be a set of rules that we force our kids to memorize until April 22 and then they aren’t supposed to think about it again?  Get with the program, will ya?

And no textbook?  C’mon, man!  What are you thinking?  Those things were all written by people who really care about making math matter to our children. Don’t you know that the more a student sits in front of a textbook, the more they learn?  I saw some research done by an independent agency Houghton, McGraw, Holt and Littell that says students can actually teach themselves with these things.

In closing, you have got it all wrong.  Kids want to have subjects forced upon them.  They want to be told the rules, they want to mindlessly copy exactly what the teacher says and does and they especially want to ask questions like, “I don’t get it.” 

Inquiry?  Yeah, right!

Sincerely,

David

p.s. Can I make a cameo in Graphing Stories vol. 2?

p.p.s Can you all help me package this up into a series of lessons?

Bridging the Gap

This one goes out to all the algebra teachers; especially those in middle school.  Anyone notice that kids “get it” in 7th grade and then act like they have never seen a variable once they hit algebra? Or am I the only one?  We had nearly 70% of our 7th graders proficient and above on last year’s CST’s, but only 40% of our algebra students were proficient.  If you take the advanced classes out of the mix, it is more like 60% to 30%.  I know, I know, you can’t base what a kid knows solely on a standardized test.  But, those numbers are pretty indicative of how the kids actually do in class.  Some will say that algebra is just too abstract for most 8th grade kids.  I don’t know if I buy that, especially when I read articles like this.  

I am going to have some release time once testing is over in order to adjust our pacing guides and I would like to be able to develop some lesson ideas to help our teachers bridge the gap between number sense and algebraic thinking.  Maybe some of you have already tackled this.  I would love to hear what you have done.  How have you sequenced your 7th grade curriculum and how have you helped move your students from numeric fluency to algebraic proficiency?  I figure if I am going to lock myself in a room and try to hash this out, you may as well be there with me!

Confessions of a 13 Year Veteran

Ok, I admit it.  My lesson planning skills suck!  It just hit me the other day. I am reading all your blogs and seeing all the cool things you are doing in your classrooms, and all I can ask myself is, “Why don’t I think of stuff like that?” 

 I think I know why.  I cut my teeth on CPM (another post on CPM coming soon) and all of my lessons were pre packaged.  All I needed to learn was to ask good questions and get out of the way.  That suited my style very well.  By the time NCLB came around and we dropped CPM, my school was already going lock step with pacing guides and common assessments.  Neither one of these approaches allowed for much innovation nor did they require a bunch of thought.  It didn’t help that I became the varsity baseball coach in my first full year of teaching and spent way more time planning practice than I did lessons.  The real problem was that I didn’t really know how much I had bitten off until recently. 

Now that I am teaching middle school math as the high school guy brought in to handle all the GATE kids, I am not only responsible for my own classes but for setting a tone and pace for an entire department.  I feel more accountability now than ever before.  It has been in these last three years that I have really started to ask reflective questions regarding not only my practice, but good practice in general.  I also have access to tools that I didn’t even know existed when I was at the high school. 

So here is a snapshot of where my lessons were compared to where they are.  Feel free to take your shots and help me make this better.  This lesson is stolen  borrowed adapted from a lesson in the April 2009 issue of Mathematics Teaching in the Middle School. 

What I would have done before:

I don’t know if I would have even bothered to re type the lesson, I may have just photo copied it and given it like this:

I would have passed out this handout and told the students to represent each savings plan as a: graph, input/output table, algebraic expression and verbal expression.  My students would have muddled through it and most would have just jumped through another hoop. 

What I did today:

I toggled between these four slides and asked students to pick out what information they thought was important.  It was interesting that some students felt it necessary to try to copy the information while the rest of the class was willing to observe and jot down what they thought was essential info.

 

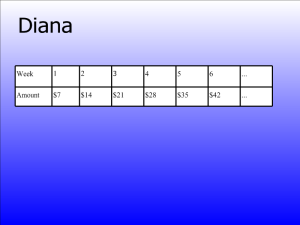
Questions students came up with:

• Does the chart represent the amount of money Diana makes each week or the total she has saved?
• Will she continue to save at this rate? “Yeah, look at the “dot, dot, dot.”

Teacher: “What can you tell me about Yoni?”

Class: “She has $300.”

Teacher: “How much will she have in 3 weeks? 2 years? 100 years?

Class: “$300. $300. $300.”

A few students were quick to point out that we only needed to focus on two or three key points in order to make a generalization of Michael’s situation.  They immediately zoomed in on (0, 30) and (10, 80).  However, I did have one group who decided to focus on the last point (20, 130). They decided that Michael averaged $6.50 per week.  But when they were asked if their trend would continue, they quickly realized that they had failed to consider the original amount of Michael’s savings.

Chandler, one of my 7th graders decided to ask, “Does x represent weeks?”  Beautiful, that info was on the next slide. 

The question of the day had to come from Paul: “So, if the only point we know for sure in Michael’s graph is (30, 80) wouldn’t he have more money if he actually started at (0,0)?  In his mind he was seeing this…

…which led to an interesting discussion on how slope represents the amount of money saved per week. 

My students are starting to catch on to how things work in my class because as soon as these slides came up:

I asked, “What is my next question?” To which they all responded:

Once they had made the decision on which represenation they prefered, I had them represent the other three savings plans the same way.

At first the justifications for “why” one representation was preferred over another were weak at best, lazy and unthoughtful at worst:

• An input/output table is more organized.
• It’s easier to see the data.
• I like it better because it is better and less worse than the others.

Okay, that last one was mine, but you get the point.  Being the father of four boys, I can smell an “alright get off my back, already” answer a mile away, I continued to prod.  Eventually we had answers like this:

• I prefer the chart because it is easier to see which numbers go together; on the graph, you have to work a little more to see which numbers are related.
• I prefer the graph because I can actually see how the different points relate.  The slope helps me see how fast someone is saving.
• I prefer the verbal expression because it helps me understand the overall situation better.

We eventually got to the discussion on “Who has the most money right now?”

Hands fly upright around the same time I hear: “Yoni! Danny!” 

Then Adrian pipes up, “When is now?”

Gotta love that kid!

Semester Project

Because my district is in program improvement, there has been a huge push to do things “one standard at a time.”  Not a bad idea since the standards (for algebra anyway) are pretty solid.  The problem lies in the fact that there is a tendency to simply teach the skills and neglect the conceptual development as well as problem solving aspect to algebra.  So I decided to call a buddy of mine who happens to be a farmer and here is a project I came up with.  I created an answer key using GeoGebra that allows for quick checking of student progress.  Feedback request: I would really like some input on this one.  I know that I would like to use it again next year, but I know it needs some work.