Personal Responsibility vs. Learning?

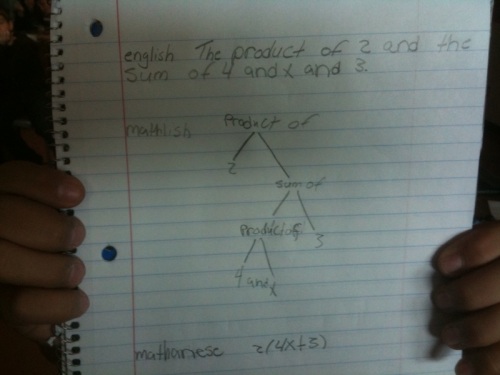
Yesterday I had a few students absent and we did a lot of examples involving multiplying binomials, factoring and solving quadratics by completing the square. It was one of those lessons that “just happened.” I had one idea I wanted to nail down and it kinda morphed into a bunch of examples. I made up most of the examples on the fly because I was just gauging their reaction and taking what they gave me. So believe me when I say, “they wasn’t the pertiest lookin’ notes ya ever did see.”

Apparently, they were effective, though. The countenance of the class went from chin-on-hand-it’s-Friday-I’m-tired-here-we-are-now-entertain-us to thank-you-sir-may-we-try-another-cuz-this-is-some-cool-stuff-and-I’m-gettin’-it.

Its tough to reproduce lessons like that so I exported the notes to .pdf and emailed them to the absent students.

I just received this email from one of the recipients:

“Thanks for the notes! They will really help. I do have one question though; did you have to take time specifically out of the lesson to take the pictures or some other program that did them for you? I’m asking this because I think that if you did this every time we learned something new and posted it on your website[s], it would be a good resource.”

So I told him I slaved over my computer all of 30 seconds to export and email as an attachment. Which leads me to my question:

I have always taken a “students gotta take responsibility for their notes and review them regularly” kind of approach which has prevented my from exporting and posting the chicken-scratch covered slides from class. But if posting them is going to help them learn, should I care about the personal responsibility they take on (or don’t take on) in regards to their own note taking?

Whatdaya think?

Note: if you’re interested in what a spur-of-the-moment-ugly-as-heck-yet-equally-effective lesson in my class looks like on static slides, hit me up in the comments and I’ll update the post with a link. I’m posting this from my phone and won’t have access to the notes until Monday.

Speaking Mathanese

Kids butcher the Mathanese language.  I’m just sayin’.  We have all these kids who speak text just fine.  It seems to me that Mathanese should be right up their alley.  All we are doing is taking a bunch of words and converting it to symbols.  Should be easy, right?  Not so much. 

I find that kids have a tough time translating algebraic expressions to English and vice versa.  Am I alone? 

Yeah, didn’t think so. 

One of the things that I have been trying to focus on this year is to convey to students the universality of the things they are learning.  For example, cause/effect in language arts becomes input/output in math.  Conflict resolution is the same as problem solving.  Language arts has expressions and sentences, so does math.  Scientific method can compare to making a conjecture in geometry, testing it out and then using inductive logic to arrive at a conclusion (read: rule). 

So what happens when you tell them to translate: the product of 3 and the sum of x and 2?

You get: 3x+2, right? 

Not quite. 

Well I figured we needed to develop a mashup of English and Mathanese; Mathglish, if you will.  Here is what we came up with:

English to Mathanese:

This should read: The product of 2 and the sum of the product of 4 and x and 3.

Mathanese to English:

The key this time was to allow the mashup.  I live in a rural area where the Spanish speaking population is very large.  Many of my kids speak and understand Spanglish.  I have never done it this way before and the kids nailed it. 

How do you do it?

Update:  Just did a quick check for understanding 2nd period and  26/28 kids circled the bases.

Joining the Fray

I’m sorry, I couldn’t help myself.  I can’t let Sean Sweeney have all the fun in class (see here and here).  I do, however, have to credit Sean with giving me the push I needed to actually do this with my class.  Thanks!

The Setup

I told my students that before the Fray was “The Fray”, they were called The Phray and their lead singer was a math teacher.  He wrote a song called “Solve to Save Your Life” but when they were signed they changed the name of the band and made some adjustments to the song on account of “math songs don’t make the top 40, baby.” It took some searching to find the archive of the old song, but I did it.  I also told them that OneRepublic had a song called “Rationalize.”  We’ll see if that one surfaces.

So with no further ado: The Phray performing their hit single, “Solve to Save Your Life.”

If you want the lyrics.

We’ll be releasing the official video soon. 

Reflection: This really isn’t my thing.  I was debating whether or not to scrap the whole thing even though my 4 yr. old can now solve equations.  The thing that really hit me was that me leaving my comfort zone allowed some of my students the freedom to do the same.  I made some connections with kids where I may not have otherwise been able to.  I also learned that playing guitar for 1.5 hours over 3 periods may cause tendonitis.  Advil anyone?

I’m Telling Ya, Lesson Plans are Overrated.

This year, I have kind of introduced equation solving to my 7th graders very informally.   One way I have done this is by giving  them a few balance equations like this:

It seems like it takes the edge off when the variable isn’t there.  But today one of our warmup problems was: 5x + 1 = 2x + 7.

I have been amazed at how many of my students have been willing to attack equation solving by using a guess and check table.  I’ve never taught it that way, but some kids have just taken to it.  After today, I may start to encourage it.  One kid noticed that when you let x=1, the right side is greater than the left side.  But if you let x=10, the left side is greater.  When the balance of power shifts, you know that the answer is between your last two guesses.  Of course, typical guess and check strategy.  But the thing I like about it when dealing with these linear equations is that they are beginning to think in terms of linear systems and how the point of intersection acts as a dividing point between which equation has greater value.  They’re teaching me something. 

But Brandon took the cake.  He says, “Mr. Cox, you can tell the left side is going to be 6 because 5+1=6 and the right side is going to be 9 because 2+7=9.”

“What does x have to be for that to be true?”

“X=1.  But as we make changes to x, the other one is growing faster.”

“How fast is it growing?”

“The left side is growing by 5 and the right side is growing by 2.  So eventually, we know that the left side is going to be greater than the right side.”

“Yeah.  So when are the 1 and the 7 important?”

“Only at the beginning.”

It took all the self control I could muster to keep from talking about initial condition or rate of change at this point.  I’m glad I didn’t because I think I would have ruined an authentic learning moment for this kid.  The thing I wanted to encourage the most in him was the fact that he looked for patterns and then asked questions to help make sense of those patterns. 

One warmup which I expected to spend 5 minutes on turns into 20 minutes of slope, y-intercept, linear systems and problem solving strategies all because a few students took an approach I’ve never taught. 

Another example of the kids re-writing the lesson plan.

What’s the point?

One of my favorite activities is to have students draw a point on a paper and see how many distinct lines they can draw through the point.  I usually set it up as a competition to see who can get the most lines inside of 15 seconds or so.  On your mark, get set, GO! Pencils start flying.

Then to bring the lesson home, I say, “Alright, flip the paper over and put two points on the page.  Now we’re gonna see who can get the most lines through both points.” 

Ready, set, GO!

They get the first line fast.  Then they panic as they move the ruler and pencil searching for that elusive second line.  Most of ’em end up looking something like this:

I tease them a bit and we all get a good chuck out of it. I know, I know.  It’s not nice to take advantage of these trusting impressionable children.  But I don’t care who you are, that thar’s funny!

 

And, they never forget it.

Stretch Factor

What does a normal parabola look like again?

And what about one with a stretch factor of 7?

And how about 1/10?

Nice job folks. 

Now get out some paper and get to work! 

And quit smiling…math ain’t that fun.